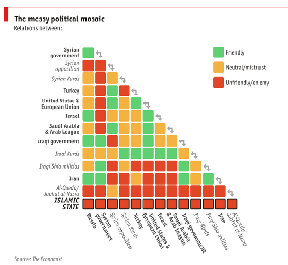
Op de website van the Economist stond gisteren een prachtig figuur, waarin de relaties tussen verschillende partijen in het Midden-Oosten weergegeven worden:
Bekijk ’m vooral even: er zijn 14 partijen die een rol spelen in het Midden-Oosten, en bij ieder van die partijen staat aangegeven of een andere partij bevriend is, neutraal, of een vijand. Al snel valt op dat de relaties niet consistent zijn. Bijvoorbeeld, volgens deze informatie is Rusland bevriend met Iran en Israël, maar staan die twee landen weer op vijandige voet met elkaar.
Ik weet niet hoe het met u is, maar als ik zo’n overzicht zie krijg ik meteen zin in matrix-algebra. Het is makkelijk om de tabel te vertalen in een 14-bij-14 matrix, waar je het getal 1 invult als de landen/groepen bevriend zijn, -1 voor vijanden en 0 voor neutraal. Voorlopig vul ik in dat een land zichzelf ook als neutraal beschouwt.
Het leuke van een matrix is dat je er allerlei berekeningen mee kunt doen. Zo kun je het kwadraat van de matrix uitrekenen, waarmee de gemiddelde band tussen groepen via een andere groep wordt weergegeven. Bijvoorbeeld: Rusland is vrienden met Iran, en Iran is vijandig met de Syrische oppositie. Via Iran is Rusland dus vijandig met de Syrische oppositie. Maar Rusland is ook tegen IS, en IS ook tegen de Syrische oppositie. Vanuit het principe “de vijand van mijn vijand” zou Rusland weer vóór de Syrische oppositie moeten zijn. Het kwadraat van de matrix geeft aan hoe de gemiddelde verhouding tussen twee landen (via derden) is. Op het kruispunt van Rusland en de Syrische oppositie staat in het kwadraat -2, wat betekent dat de twee partijen elkaar vaker als vijand zien dan als bondgenoot. Dat klopt met de directe verhouding tussen de twee, zoals blijkt uit het diagram is die ook vijandig.
Het is aardig om bij iedere cel in het originele diagram te kijken of het teken (vriend/neutraal/vijand) overeen komt met de indirecte relatie. Er is sprake van een clash als de één vriendschappelijk is, en de ander vijandig. Slechts twee landen hebben helemaal geen clash: Rusland en de Iraakse Koerden. Die zijn dus vooral vrienden met de vrienden van hun vrienden, of vrienden met de vijanden van hun vijanden. De meest inconsistente partijen zijn Al Qaida en IS, die met iedereen ruzie hebben, en de Syrische Koerden. Die laatste groep maakt ruzie met onder meer Turkije en Iran, terwijl dat via-via meer bondgenoten zouden zijn.
Er is nog een andere transformatie mogelijk die iets aardigs laat zien. Hiervoor gebruik ik een matrix met het getal 1 op de diagonaal, in plaats van het getal 0. Dat betekent dus dat landen zichzelf als vriend beschouwen. (Dat klinkt logisch. In de vorige versie gebruikte ik dit gegeven niet zodat we met het kwadraat puur via andere landen konden kijken.)
Als we de matrix met enen inverteren, dan kunnen we een vergelijking van het soort Ma=b oplossen. Dit helpt bij het beantwoorden van de vraag wie een land/groep zou moeten steunen, om er zelf beter van te worden. Als we voor b bijvoorbeeld de vector [1 0 0 0 ..]’ invullen, en dan met de inverse a berekenen, dan zou a iets moeten zeggen over de groepen die Rusland moet steunen of dwarszitten om er zelf beter van te worden. Het antwoord daarop is gecompliceerd: Rusland moet onder meer Iran en de Syrische Koerden steunen, en de Iraakse Koerden en de Syrische regering dwarszitten.
En wat zou onze eigen groep, de US/EU moeten doen? Volgens deze matrix moeten we Israël, de Iraakse regering én de Iraakse Shia-milities steunen, en Iran en de Syrische Koerden dwarszitten. Dat laatste onder meer om Turkije te compenseren voor de gevolgen van de andere acties.
Voor klachten over de praktische logica en implementeerbaarheid van dit advies moet u overigens niet bij mij zijn – ik reken alleen maar wat dingen uit. Wilt u zelf ook rekenen, dit is de matrix met nullen op de diagonaal:
| R | Sg | So | Sk | T | W | Isr | SA | Ig | Ik | Is | Ir | AQ | IS | |
| Russia | 0 | 1 | -1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | -1 | -1 |
| Syrian govt | 1 | 0 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 0 | 1 | 1 | -1 | -1 |
| Syrian opposition | -1 | -1 | 0 | 0 | 1 | 1 | 0 | 1 | -1 | 0 | -1 | -1 | 0 | -1 |
| Syrian kurds | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | -1 | -1 |
| Turkey | 0 | -1 | 1 | -1 | 0 | 1 | 0 | 0 | 0 | 1 | -1 | 0 | -1 | -1 |
| US&EU | 0 | -1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
| Israel | 1 | -1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | -1 | -1 | -1 | -1 |
| Saudi & Arab league | 0 | -1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | -1 | -1 | -1 | -1 |
| Iraqi govt | 1 | 1 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | -1 | -1 |
| Iraqi kurds | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | -1 |
| Iraqi Shia militias | 0 | 1 | -1 | 0 | -1 | -1 | -1 | -1 | 1 | 0 | 0 | 1 | -1 | -1 |
| Iran | 1 | 1 | -1 | -1 | 0 | -1 | -1 | -1 | 1 | 0 | 1 | 0 | -1 | -1 |
| Al Qaida | -1 | -1 | 0 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 0 | -1 |
| IS | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 0 |

Zou je niet eigenlijk naar de Leontief inverse moeten kijken? Of is dat wat je dit door enen op de hoofddiagonaal te zetten?
Ik denk het niet. Als ik me goed herinner is bij IO-analyse de matrix opgebouwd uit positieve getallen die optellen tot iets kleiner dan 1: input shares. Door de Leontief inverse te nemen neem je (tot in het oneindige) de benodigde inputs mee. Die som convergeert omdat de elementen van de matrix kleiner dan 1 zijn.
Deze (simpele) inverse kijkt maar naar een eenmalig effect: door 1/2 aan Rusland te geven breng je een slag van -1/2 aan de Syrische oppositie toe. Dat werkt vast ook door op (bijvoorbeeld) de Syrische regering, maar voor dat soort 2e orde effecten zou je iets anders in de matrix willen hebben dan enen en min-enen, anders convergeert het nooit.
Het is vast mogelijk om dat soort fracties te verzinnen als je nog meer verstand van internationale relaties hebt.
Ah ja, daar kun je wel eens gelijk in hebben, dat gaat niet convergeren.