Toen uw verslaggever onlangs via de sluizen aan de noordzijde de Afsluitdijk opreed, viel zijn oog op dat bordje dat bij elke grote ophaalbrug in Nederland staat: slagbomen dalen automatisch. Een schijnbaar nutteloze mededeling over de rood-witte boom, die nu keurig in verticale positie stond.
Maar de Afsluitdijk is lang en nodigt de berijder uit tot diepe gedachten, en zo kwam het dat ik mij plotseling iets voor kon stellen bij het mysterieuze bordje. Iets economisch, zelfs. In mijn enthousiasme trapte ik het gaspedaal nog wat verder in, zodat ik eerder achter mijn bureau zou zitten om mijn ingeving na te rekenen. En wat blijkt: het klopt! Dit bedacht ik mij:
Een neerkomende slagboom is een vreselijk iets, een soort op-rood-springend stoplicht, maar dan erger. De automobilist die de boom voor zich ziet dalen weet dat hij of zij de komende vijf tot 10 minuten stil gaat staan, in plaats van zich voort te bewegen richting bestemming. Dat maakt het interessant om de neerkomende boom te negeren. Ervan uitgaande dat de brugbediende er geen trek in heeft een autowrak onder zijn boom op te ruimen, kan het haast niet anders of hij wacht even totdat de ongehoorzame doorrijder voorbij is. Tegelijkertijd is dat een probleem: als iedereen er zo over denkt kan de brug natuurlijk nooit open.
Wat we hier hebben is een geval waarin de brugwachter en de automobilist strategisch gedrag vertonen: ze handelen beiden tegelijk, en de actie van de één heeft gevolgen voor de uitkomst van de ander. Zulk gedrag is goed te analyseren met behulp van een favoriete bezigheid van microeconomen, de speltheorie. Om te beginnen kunnen we de hele situatie weergeven in een payoff matrix, waarin alle mogelijke uitkomsten staan. Iedere speler heeft twee keuzes: de brugwachter kan de slagboom laten zakken of even wachten (horizontaal), de autorijder kan doorrijden of stoppen (verticaal).
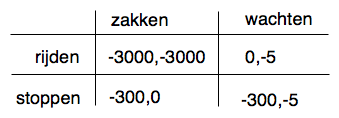
In de matrix staat voor elke combinatie van acties hoeveel tijd het de participanten oplevert, eerst de automobilist en dan de brugwachter. Rijdt de automobilist door en wacht de brugwachter (rechtsboven), dan verliest de laatste 5 seconden en de eerste niks. Stopt de automobilist, dan verliest hij 5 minuten. De brugwachter verliest niks als hij dan meteen de boom dichtdoet (linksonder), of 5 seconden als hij toch nog even wacht (rechtsonder). Zijn beiden koppig, dan gaat de auto tegen de boom en verliezen alle partijen 50 minuten (linksboven).
Een (Nash)-evenwicht is het als geen speler erop vooruit gaat door van actie te veranderen, gegeven de acties van anderen. In dit geval zijn er twee: wachten-rijden en stoppen-zakken. Gegeven dat de auto doorrijdt kan de brugwachter beter even wachten, gegeven dat de brugwachter wacht kun je beter doorrijden. En vice versa. Qua spelstructuur (en misschien wel meer) is dit gelijk aan the game of Chicken, waarbij de eerste die toegeeft verliest.
Vervelend, die twee mogelijke uitkomsten. Rationeel is niet te voorspellen welk evenwicht zich manifesteert; omdat coördinatie moeilijk is kan een misverstand zomaar voorkomen, met een crash als resultaat.
Wat ons brengt bij het bordje. Het spel is namelijk te winnen door niet rationeel te zijn, door in ieder voorkomend geval dezelfde strategie te spelen, zelfs als dat voor jezelf niet optimaal is. Als je als brugwachter geloofwaardig kunt stellen dat je nooit toegeeft, door bijvoorbeeld je handen op de rug te binden, verandert het spel. Het bordje geeft aan dat de brugwachter gek is, en dus heeft de automobilist de keuze: stoppen (-300) of doorrijden (-3000). De automobilist stopt en de brugwachter wint.
Briljant!