Ja, waarom gebruiken economen eigenlijk omgekeerde assen, waarbij we de prijs verticaal zetten en de hoeveelheid horizontaal (zie bijvoorbeeld hieronder)? Is dat inderdaad historisch bepaalde onzin?
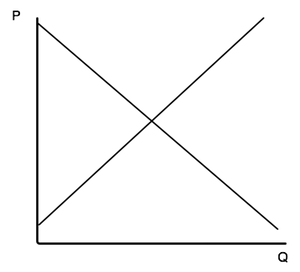
De eerste reactie van de verdachte is natuurlijk ontkennen. Het is gebruikelijk om de onafhankelijke variabele horizontaal te zetten en de functie van die variabele verticaal, waarbij het vaak zo is dat de één de ander bepaalt. De assen zijn verkeerd om, stelt men, want vraag en aanbod worden bepaald door de prijs. Maar dat is niet noodzakelijk. Neem aanbod vraag: als ik een vast aantal kerstbomen heb om te verkopen, dan zal ik mijn prijs zo zetten dat ik ze precies allemaal kwijtraak. De aanbod hoeveelheid bepaalt dan de prijs en de assen staan goed.
Maar er is nog een betere reden om het diagram zo te tekenen. Degene die de conventie historisch bepaald heeft is de Engelsman Alfred Marshall. Hij geldt ook als een van de grondleggers van het begrip surplus. Het surplus in een marktevenwicht geeft aan hoeveel waarde er gecreëerd wordt, bovenop de productiekosten. Dat kun je uittekenen in het diagram:
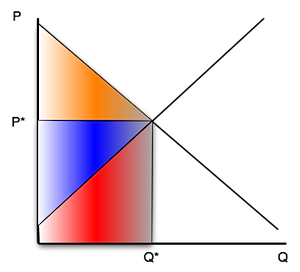
De prijs die tot stand komt is P*, de verhandelde hoeveel Q*. De (variabele) productiekosten worden weergegeven door het rode oppervlak. Blauw is het producentensurplus: het geeft aan dat bepaalde producenten ook voor minder hadden willen verkopen, en dus een extraatje krijgen. Oranje is het consumentensurplus, idem geeft dat aan dat bepaalde consumenten meer hadden willen betalen dan de marktprijs, en dus voordelig uit zijn.
Bij wiskunde leer je dat je oppervlaktes kunt bepalen met een integraal. Dat kan ongeacht de stand van de assen, maar het makkelijkst is het als je een oppervlakte onder een curve over een stukje van de x-as moet bepalen. Door de prijs op de verticale as te zetten kun je dus het surplus makkelijk berekenen.
Ik heb geen idee of Marshall het daarom zo bedacht heeft, maar aannemelijk is het wel.



